astro

Dans cette note, on calcule la position (azimut) du lever de soleil vu d'un point élévé de la Terre, et en particulier, à titre d'application, vu du Pic de Saint-Barthélémy en Ariège.

Etant donnés la complexité du phénomène et le nombre de paramètres mis en jeu, il serait difficile de parvenir une très grande précision pour la prédiction de ce phénomène en gardant un volume de calculs raisonnable. L'objectif du calcul présenté ici est de ne tenir compte que des paramètres principaux, afin d'obtenir une erreur inférieure à un quart de diamètre solaire.

Pour la partie astronomique des calculs on suppose une orbite circulaire une Terre sphérique. Pour ce calcul, on tient compte, de manière simplifiée de l'altitude du point d'observation et de l'effet moyen de la réfraction atmosphérique. Ces deux effets sont ceux qui peuvent modifier le plus substantiellement la position de soleil à son lever, par rapport à un calcul purement "astronomique", c'est à dire géométrique. Les modifications dues à ces deux effets engendrent une déviation en azimut équivalente à plusieurs jours de décalage du soleil. Pour ces calculs on néglige les effets dus aux possibles variations dans les conditions de réfraction atmosphérique le jour de l'observation en ne retenant que la réfraction par une atmosphère moyenne. Enfin, on suppose que le point d'observation est situé dans l'hémisphère nord.

1 Introduction

Le but premier que se fixe cette note est d'être capable de prévoir la date à laquelle il faut se placer en un point d'observation donné (le sommet du Pic de Saint-Barthélemy par exemple) pour pouvoir observer le soleil se lever en un autre point de la Terre donné lui aussi. De cet objectif premier découle aussitôt une conséquence évidente: il est souhaitable que la précision du calcul de l'azimut du soleil à son lever soit inférieure à, disons, un quart de diamètre solaire. Ainsi on sera sûr qu'une bonne partie du disque solaire se détache effectivement en contre-jour sur la silhouette du point visé.

Il faut bien voir toutefois qu'une estimation très précise de l'azimut du soleil à son lever (avec, disons, une précision de l'ordre d'un centième de diamètre solaire), serait assez difficile à obtenir, et donnerait lieu à des calculs assez ardus et couteux. Mais tel n'est pas le but visé ici, et les calculs peuvent donc rester relativement simples.

La détermination de l'azimut su soleil à son lever est un problème qui grosso modo peut se décomposer en deux sous problèmes relativement indépendants: la partie "astronomique" des calculs, afin de pouvoir déterminer l'azimut et la hauteur du soleil en fonction du temps; et la partie "terrestre" des calculs afin de déterminer la position précise (en azimut et site) du point observé, puis du soleil lorsqu'il se détache optiquement sur ce point.

Dans chacune des deux parties du calcul, on est obligé de faire des approximations si on veut garder des calculs assez simples. Néanmoins, il semble qu'il soit possible de concilier à la fois une simplicité raisonnable pour les calculs et une précision de l'ordre de celle visée dans les objectifs premiers ci-dessus, c'est à dire un quart de diamètre solaire pour la direction de l'azimut au lever.

Pour la partie astronomique on fait principalement deux hypothèses simplificatrices: d'abord, on néglige les irrégularités de l'orbite terrestre en considérant simplement une orbite circulaire parfaite que la Terre décrit d'un mouvement uniforme. Ensuite, l'inclinaison de l'écliptique (ou encore obliquité de la terre sur son orbite) notée $\delta$ est supposée constante. Cet angle $\delta$ est l'angle entre l'axe de rotation diurne de la Terre et la normale au plan de l'orbite terrestre (appelé écliptique car c'est lorsque la lune est dans ce plan que peuvent avoir lieu les éclipses). En fait l'axe de rotation de la Terre est sujet à des variations au cours du temps, mais sur des périodes tellement longues qu'on paut sans aucun mal les négliger ici: l'angle $\delta$ peut varier de $\pm 1.3^\circ$ au cours du temps, ce qui est important, mais la périodicité de ces variations est d'environ 41000 ans. Actuellement (et pour plusieurs milliers d'années) $\delta$ est dans une période de décroissance, à un rythme de $0.016^\circ$ en 125 ans ! On voit donc que cet aspect relatif aux variations temporelles de $\delta$ peut être purement et simplement négligé pour ce qui nous occupe ici (à moins de programmer dès aujourd'hui une excursion pour le 21 Juin 24876 !). Grâce à ces deux hypothèses principales , tous les calculs astronomiques se réduisent à des calculs de géométrie sphérique relativement simples.

Pour la partie terrestre, le problème se décompose lui-même en deux sous problèmes, de nature géodésique et optique: En effet, il faut d'abord être capable d'estimer la position géométrique précise du point que l'on veut viser. On suppose ici que le point d'observation et le point visé sont connus par leur coordonnées longitude/latitude et par leur altitude. Il s'agit donc de déterminer l'azimut et le site "géométriques" du point visé. Ici, et dans toute cette note le mot "géométrique" appliqué au site et à l'azimut signifie que le rayon de visée est supposé être une droite, c'est à dire que la réfraction atmosphérique est négligée. La détermination très précise du site et azimut du point visé à partir des coordonnées géographiques pose des problèmes complexes du fait que la Terre n'est pas une sphère, mais un géoïde irrégulier (même si on rabotait tous les reliefs au niveau de la mer). Ici on fait donc l'hypothèse que la Terre est simplement une sphère parfaite (c'est à dire que la surface située au niveau de la mer est une sphère parfaite). Les effets de cett hypothèse sont probablement très faibles, mais en revanche elle permet de réduire tous les calculs de géodésie à des calculs de géométrie sphérique relativement simples. Ensuite la partie terrestre des calculs il reste un problème de nature optique, puisque la présence de l'atmosphère engendre une courbure des rayons optiques. La direction de visée effective (ou "optique" dans cette note) diffère donc de la direction de visée "géométrique" évoquée ci-dessus. A cause de la réfraction atmosphérique tous les objets visés sont sujets à une déviation différente selon leur distance et leur altitude. Ainsi, même si deux objets sont alignés optiquement pour un observateur donné, les deux rayons de visée n'ont pas nécessairement la même déviation. En particulier, pour le soleil au lever, le rayon lumineux issu du soleil est toujours plus dévié que le rayon lumineux issu du point de l'horizon où le soleil émerge. Pour la partie "optique" des calculs, on fait les hypothèses simplificatrices suivantes sur l'indice de réfraction de l'air: on néglige le rôle de la vapeur d'eau contenu dans l'air, on néglige le rôle de la longueur d'onde lumineuse, et on néglige les fluctuations atmosphériques pour ne considérer l'atmosphère que dans un état moyen de température et de pression, ne dépendant que de l'altitude (appelé "atmosphère standard"). Grâce à ces hypothèses, le calcul de la déviation des rayons lumineux peut être effectué relativement simplement (mais au prix d'un programme informatique toutefois).

2 Géométrie du problème

Dans tout ce document, on se place uniquement en géométrie sphérique sur une sphère de rayon arbitraire représentant l'espace visuel au point d'observation, c'est à dire essentiellement la voûte celeste et l'horizon. L'espace visuel qui nous intéresse réellement est donc grosso-modo une demi-sphère (mais pas tout à fait car le point d'observation est en altitude et donc l'horizon est situé sous l'horizontale du lieu d'observation). Un point de l'espace visuel peut donc être repéré par deux nombres, qui dans un système de coordonnées sphériques sont baptisées longitude et latitude.

Deux systèmes de coordonnées sphériques particuliers seront utiles pour effectuer nos calculs: d'abord le système de coordonnées sphériques "azimutal", dans lequel le plan horizontal de l'observateur est l'origine des latitudes; ensuite le système de coordonnées sphériques "équatorial", dans lequel l'équateur céleste est l'origine des latitudes. Comme ces deux systèmes sont utiles "à tour de rôle" pour les calculs, il faut nécessairement connaitre les formules de transformations directes et inverses qui permettent de passer du premier au second et vice-versa.

2.1 Coordonnées azimutales

Dans ce système de coordonnées, un point de l'espace visuel est repéré par une longitude "azimutale" $\lambda$ (supposée nulle au sud et comptée positivement en allant vers l'est) et par une latitude "azimutale" $\theta$ (supposée nulle sur le plan horizontal de l'observateur et comptée positivement vers le haut). On voit donc que dans ce système de coordonnées, le plan de l'horizontale relatif à l'observateur est l'origine des latitudes, décrit par $\theta=0$ .

On peut définir les quatre points cardinaux relatifs à l'observateur, qui sont: le "midi"

(au sud et à l'horizontale de l'observateur), le levant

(à l'est), le septentrion

(au nord) et le ponant

à l'ouest. de plus, le zénith

est le point qui se trouve à la verticale de l'observateur. On a donc les coordonées suivantes:

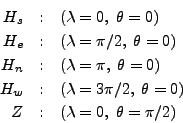
$\begin{eqnarray*} H_s & : & (\lambda = 0, \; \theta=0) \\ H_e & : & (\lambda = ... ... \pi/2, \; \theta=0) \\ Z & : & (\lambda = 0, \; \theta=\pi/2) \end{eqnarray*}$

2.2 Coordonnées équatoriales

Ce système de coordonnées est un peu plus complexe à définir que le précédent, puisqu'il prend en compte l'inclinaison de l'équateur céleste. Soit $\mu_0$ la latitude géographique du lieu d'observation (pour le Pic de Saint-Barthélemy, on a $\mu_0 = 42.82^\circ = 0.7473$ Rad). Le pôle nord céleste (PNC) est le point dont les coordonnées azimutales sont:

$\displaystyle \lambda_p$	$\textstyle =$	$\displaystyle \pi$	(1)
$\displaystyle \theta_p$	$\textstyle =$	$\displaystyle \mu_0$	(2)

C'est autour de ce point que s'effectue la rotation diurne des astres fixes. L'équateur céleste est le lieu de tous les points de la sphère qui sous-tendent un angle droit par rapport au pôle nord céleste. Le point

de l'équateur céleste qui est en direction du sud (avec $\lambda=0$ donc), possède une latitude azimutale égale à $\pi/2 - \mu_0$ , et pour le point

de l'équateur céleste situé dans la direction nord, la latitude azimutale est $3 \pi / 2 - \mu_0$ . Les points

de l'équateur céleste situés respectivement à l'est et à l'ouest ont une latitude azimutale nulle (il sont dans le plan horizontal de l'observateur). Etant donnés ces éléments, on définit le système de coordonnées sphériques équatoriales $(\lambda', \theta')$ comme les coordonées sphériques pour lesquelles l'origine des latitudes est l'équateur céleste. Plus précisément, les longitudes équatoriales sont comptées à partir de sud et positivement vers l'est, tandis que les latitudes équatoriales sont comptés positivement de l'équateur céleste en allant vers le pôle nord céleste PNC. En conséquence, dans ces nouvelles coordonnées, l'équation de l'équateur céleste est $\theta'=0$ et les coordonnées du point PNC sont $(\lambda'_p = 0, \; \theta'_p=\pi/2)$ , la valeur de la longitude étant là encore purement conventionnelle pour ce dernier point.

2.3 Nécessité des formules de transformation

Pour les dix points remarquables que sont

, et

, on peut déterminer assez facilement les coordonnées azimutales et équatoriales de manière graphique sur un schéma, ce qui donne:

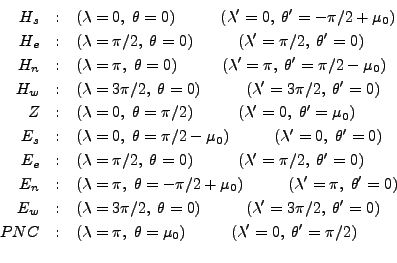
$\begin{eqnarray*} H_s & : & (\lambda = 0, \; \theta=0) \hspace{1cm} (\lambda' = ... ... \theta= \mu_0) \hspace{1cm} (\lambda' = 0, \; \theta'=\pi/2)\\ \end{eqnarray*}$

En revanche pour un point quelconque, la détermination graphique des coordonnées azimutales connaissant les coordonnées équatoriales (ou vice-versa) n'est pas aisée. On utilise alors des formules de transformations issues de la géométrie analytique, discipline qui permet notamment de définir les nouvelles coordonnées d'un point donné de l'espace si on lui fait subir une rotation donnée dans l'espace. En effet les deux systèmes de coordonnées azimutal et équatorial se déduisent l'un de l'autre par une simple rotation autour de l'axe est-ouest.

2.4 Formules de transformation générales entre deux systèmes de coordonnées sphériques

Pour information, nous donnons les formules de transformation pour une rotation plus générale que celle dont nous aurons besoin ici. Le lecteur pressé peut donc sauter cette section sans dommage.

Si $(\lambda, \theta)$ sont les coordonées azimutales d'un point donné, ses nouvelles coordonnées $(\lambda', \theta')$ dans un système de coordonnées sphériques général qui a pour "pôle supérieur" le point de coordonnées $(\lambda=\lambda_p, \theta=\theta_p>0)$ et pour lequel le zénith de l'observateur se retrouve sur le méridien origine $(\lambda'_Z=0$ ) sont données par:

$\begin{eqnarray*} \theta' & = & \arcsin \left[\sin \theta_p \sin \theta + \cos \... ...eta'}\right)\left[\cos \theta \sin (\lambda - \lambda_p) \right] \end{eqnarray*}$

$\begin{eqnarray*} \theta & = & \arcsin \left[\sin \theta_p \sin \theta' + \cos \... ...1}{\cos \theta } \right)\left[\cos \theta' \sin \lambda' \right] \end{eqnarray*}$

Pour plus d'information sur l'origine de ces deux formules, voir le lien suivant (téléchargement d'un fichier PostScript):

2.5 Formules de transformation entre coordonnées azimutales et équatoriales

Dans le cas qui nous intéresse ici, qui est de passer des coordonnées azimutales aux coordonnées équatoriales, la transformation est moins générale, donc plus simple. La raison est que la position du "pôle supérieur" des nouvelles coordonnées (équatoriales) n'est pas quelconque, mais donnée par (1)-(2). Dans ce cas particulier on a donc:

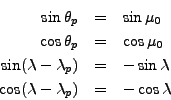
$\begin{eqnarray*} \sin \theta_p & = & \sin \mu_0 \\ \cos \theta_p & = & \cos \m... ...sin \lambda \\ \cos (\lambda - \lambda_p) & = & - \cos \lambda \end{eqnarray*}$

En conséquence, en reportant dans la formule générale, la formule de transformation directe qui nous intéresse s'écrit:

$\displaystyle \theta'$	$\textstyle =$	$\displaystyle \arcsin \left[\sin \mu_0 \sin \theta - \cos \mu_0 \cos \theta \cos \lambda \right]$	(3)
$\displaystyle \cos \lambda'$	$\textstyle =$	$\displaystyle \left(\frac{1}{\cos \theta'}\right)\left[\cos \mu_0 \sin \theta + \sin \mu_0 \cos \theta \cos \lambda \right]$	(4)
$\displaystyle \sin \lambda'$	$\textstyle =$	$\displaystyle \left(\frac{1}{\cos \theta'}\right)\left[\cos \theta \sin \lambda \right]$	(5)

$\displaystyle \theta$	$\textstyle =$	$\displaystyle \arcsin \left[\sin \mu_0 \sin \theta' + \cos \mu_0 \cos \theta' \cos \lambda' \right]$	(6)
$\displaystyle \cos \lambda$	$\textstyle =$	$\displaystyle - \left(\frac{1}{\cos \theta } \right)\left[\cos \mu_0 \sin \theta' - \sin \mu_0 \cos \theta' \cos \lambda' \right]$	(7)
$\displaystyle \sin \lambda$	$\textstyle =$	$\displaystyle - \left(\frac{1}{\cos \theta } \right)\left[\cos \theta' \sin \lambda' \right]$	(8)

On vérifie facilement que les correspondances pour les dix points remarquables ci-dessus sont bien reproduites par ces formules.

3 Déclinaison du soleil et equation du mouvement

Il faut maintenant écrire l'équation du mouvement décrit par le soleil au cours du temps, pour savoir où il se trouve au moment de son lever. Pour cela il faut connaître à chaque instant la déclinaison solaire, c'est à dire la hauteur angulaire du soleil par rapport au plan de l'équateur céleste. Nous écrivons cette formule en fonction du jour de l'année

, compté à partir de l'équinoxe de printemps (où

), jusqu'à 365.25. On notera que pour un calcul assez précis, il faut connaître l'heure de l'équinoxe et définir

non pas comme un nombre entier, mais comme un nombre réel. L'équinoxe est par définition le moment ou $\theta'=0$ et l'heure des équinoxes et des solstices est généralement portée sur tous les bons calendriers (au moins ceux de la Poste). Pour pouvoir calculer

avec une précision suffisante pour notre problème c'est à dire avec au moins un chiffre derrière la virgule, il faut connaître, même approximativement l'heure du lever du soleil. Si on se borne à compter le nombre de jours écoulés depuis l'équinoxe, l'erreur sur l'azimut solaire au lever pourra atteindre un angle égal au déplacement du soleil levant entre deux jours consécutifs, ce qui peut réprésenter un diamètre solaire. C'est pour cette raison qu'il faut calculer

avec au moins un chiffre significatif après la virgule.

On notera que si on est plus intéressé par des dates proches de l'équinoxe d'automne, on pourra définir

comme ayant pour origine le moment de l'équinoxe d'automne (toujours sur le calendrier) , et utiliser ce

à la place de

, comme indiqué ci-dessous.

Ensuite, nous supposerons que l'inclinaison de l'orbite terrestre reste constante, et égale à sa valeur moyenne $\delta = 23.44^\circ$ . Comme expliqué dans l'introduction, $\delta$ varie au cours du temps, mais tellement lentement que cela n'a aucune incidence pratique pour ce qui nous occupe ici.

Enfin, on peut se contenter d'utiliser l'hypothèse d'une orbite circulaire parfaite pour la Terre. Dans ce cas on montre facilement que la déclinaison solaire varie selon la formule suivante:

$\begin{displaymath} \sin \Delta(j) = \sin \delta . \sin(2 \pi j / 365.25) , \end{displaymath}$

(9)

Alors en coordonnées sphériques équatoriales, la latitude équatoriale du soleil à l'instant "j", est donnée par:

Au voisinage d'un instant

donné, la trajectoire di soleil coïncide à très peu près avec le cercle de la voute céleste défini par $\theta'=\Delta(j)$ , car $\Delta(j)$ varie très lentement au cours du temps et notamment au cours d'une révolution diurne.

Pour des dates plus proches de l'équinoxe d'automne, il est préférable d'utiliser:

$\begin{displaymath} \sin \Delta(j') = - \sin \delta . \sin(2 \pi j' / 365.25) , \end{displaymath}$

(11)

4 Azimut du soleil à son lever (calcul purement géométrique)

Dans cette section on calcule l'azimut du soleil à son lever sans tenir compte de l'élévation du point d'observation ni de la réfraction atmosphérique, et donc on se borne à un calcul purement astronomique ou géométrique. Dans ce cas, le lieu du lever du soleil est déterminé par le fait que $\theta=0$ . Pour connaître l'azimut de ce lieu, il suffit donc de reporter les valeurs $\theta=0$ et $\theta'=\Delta(j)$ dans l'équation (3). On obtient:

$\begin{displaymath} \cos \lambda = - \frac{\sin \Delta(j)}{\cos \mu_0} \end{displaymath}$

(12)

Ceci suffit à déterminer complètement l'azimut $\lambda$ car celui ci est borné entre

et $\pi$ (le soleil se lève toujours du côté est de l'horizon).

5 Azimut du soleil à son lever en altitude (calcul géométrique)

Lorsqu'on observe le lever de soleil d'un point élevé, deux effets viennent substantiellement modifier l'azimut observé: lélevation du point d'observation et la réfraction atmosphérique. Dans cette section on tient compte de l'élévation en négligeant lé réfraction. Comme le point d'observation est en altitude, l'horizon terrestre est abaissé et se retrouve plus bas que le plan horizontal local, et puisque la trajectoire du soleil n'est pas verticale à son lever (dès que l'observateur ne se trouve pas sur l'équateur), cela modifie l'azimut du soleil par rapport à une observation en plaine.

Pour tenir compte de l'impact de l'élevation sur l'azimut au lever, il suffit de remplacer la condition $\theta=0$ valable pour un observateur au niveau de la mer, par la condition $\theta= \beta_0$ , où $\beta_0$ (négatif par convention) est le site de l'horizon géometrique au point d'observation, c'est à dire l'angle (négatif) que fait l'horizon terrestre avec le plan horizontal. En effet, le soleil se lèvera lorsque son site sera égal à celui de l'horizon et non pas lorsque son site sera nul. Si on tient compte de l'élevation seule sans la réfraction, l'azimut du soleil au lever est donc donné par:

$\begin{displaymath} \cos \lambda = \tan \mu_0 \tan \beta_0- \frac{\sin \Delta(j)}{\cos \mu_0 \cos \beta_0} \end{displaymath}$

(13)

6 Azimut du soleil à son lever (calcul complet)

Lorsqu'on observe le lever de soleil d'un point élevé, deux effets viennent substantiellement modifier l'azimut observé. D'une part, comme le point d'observation est en altitude, l'horizon terrestre est abaissé et se retrouve plus bas que le plan horizontal local, et puisque la trajectoire du soleil n'est pas verticale à son lever (dès que l'observateur ne se trouve pas sur l'équateur), cela modifie l'azimut du soleil par rapport à une observation en plaine. D'autre part, la réfraction atmosphérique rehausse le soleil davantage que l'horizon apparent, en conséquence de quoi, lorsque le soleil se lève "optiquement" il est "géométriquement" encore caché sous la terre. Ce second effet est discuté en détail dans le lien suivant:

haussement du soleil à son lever par la réfraction atmosphérique
Ensuite, pour tenir compte en plus de la réfraction, il faut calculer la valeur de $\theta$ lorsque les deux effets sont présents. Pour cela, il faut trouver quelle est la latitude azimutale $\theta$ exacte du soleil au moment de son lever. C'est un peu plus compliqué que dans le cas précédent car le rayon lumineux issu du soleil est maintenant courbé. Nous reproduisons ici la figure présentée lors des calculs sur la réfraction, et qui permet de comprendre aisément quelle est la latitude azimutale du soleil lors de son lever.

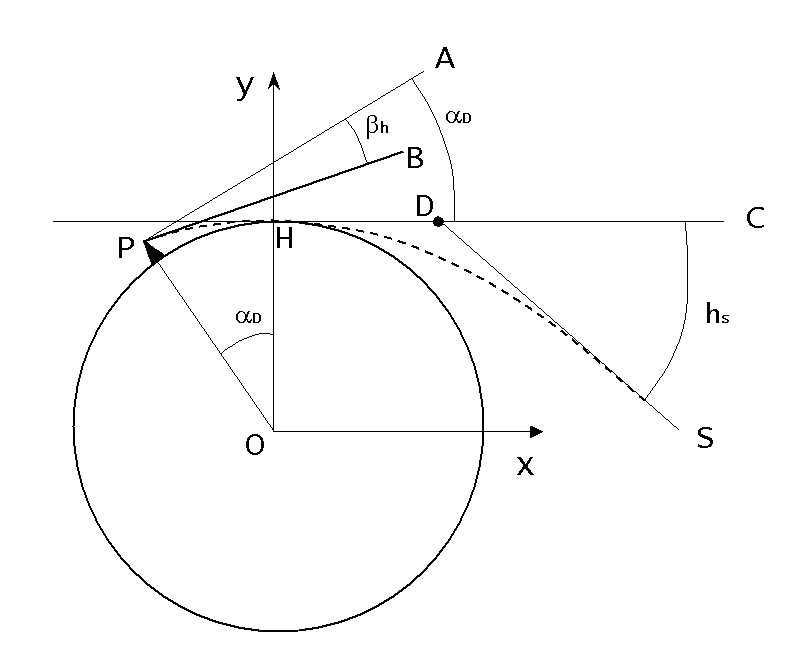
L'observateur est placé en

au sommet de la montagne. Le soleil est matérialisé par le point

, rejeté à l'infini. La courbe en pointillé représente le trajet du rayon lumineux au moment du lever du soleil. Au delà d'une certaine altitude, cette courbe devient une droite car la raréfaction de l'air fait que l'indice de réfraction tend vers celui du vide. Le point

est le point où le rayon lumineux rencontre la surface terrestre, c'est donc l'horizon optique pour le point d'observation considéré. L'angle $\alpha_D$ (compté positivement) est la distance angulaire terrestre entre les points

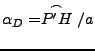, donc $\alpha_D = \stackrel{\frown}{P'H} / a$ où

est le rayon terrestre et $\stackrel{\frown}{P'H}$ est la longueur de l'arc

étant la projection de

au niveau de la mer le long de la verticale locale. On voit que le plan de l'horizontale locale pour l'observateur est la droite

sur la figure, et que cette droite fait un angle $\alpha_D$ avec la droite

. Ensuite, le soleil au moment de son lever est dans la direction

qui fait un angle

(compté positivement) avec la droite

. La latitude azimutale $\theta$ du soleil au moment de son lever est donc l'angle (négatif):

Pour trouver l'azimut solaire à son lever en tenant compte à la fois de l'élevation et de la réfraction, il suffit de substituer non plus $\theta=0$ , mais $\theta=- (\alpha_D + h_s)$ dans l'équation (3). On obtient alors:

$\begin{displaymath} \cos \lambda = - \tan \mu_0 \tan (\alpha_D + h_s) - \frac{\sin \Delta(j)}{\cos \mu_0 \cos (\alpha_D + h_s)} \end{displaymath}$

(15)

Comme précédemment, ceci suffit à déterminer complètement l'azimut $\lambda$ car celui ci est borné entre

et $\pi$ .

7 Remarques

1) On aurait pu touver tous les résultats de ce document sans passer par la géométrie analytique, mais en utilisant des raisonnements de géométrie élémentaire, c'est à dire simplement en traçant des figures, mais une telle approche nécessite un bon sens "géométrique" pour ce qui est la géométrie sphérique dans l'espace, sens qui n'est pas partagé par tout le monde. De plus, cela entraine des figures assez délicates à réaliser. C'est pourquoi une approche plus analytique, donc plus facile à suivre pour le lecteur a été choisie ici.

2) Le calcul de $\alpha_D$ , dépendant lui-même de l'élevation et de la réfraction, est relativement complexe à réaliser de manière précise. Cela nécessite un programme informatique tel que celui décrit sur le lien des calculs de réfraction indiqué ci dessus. Néanmoins, si on ne dispose pas de ce programme, on peut, pour des points d'observation raisonnablement peu élevés comme les Pyrénées, approximer sans commettre une erreur trop grossière, la distance de l'horizon optique

par la distance de l'horizon géométrique. Ceci donne alors pour $\alpha_D$ une valeur proche de $\sqrt{2 z_0 / a}$ où

est l'altitude du point d'observation. Néanmoins on peut voir dans la section 8 ci-dessous que l'impact typique de cette approximation pour une montagne de 2300 m est de 1/4 de diamètre solaire, ce qui n'est pas tout à fait négligeable lorsqu'il s'agit de déterminer l'azimut précisément.

3) En revanche la valeur de

est, dans les hypothèses choisies ici une constante "universelle". C'est la déviation verticale des rayons du soleil au moment de son lever, qui est donnée (sous nos hypothèses) par:

4) Dans la formule complète (15) le facteur $\cos (\alpha_D + h_s)$ au dénominateur du dernier terme joue un rôle tout à fait négligeable dans les circonstances qui nous intéressent, où $\alpha_D$ et

sont des angles très petits. L'interprétation géométrique de ce facteur n'est véritablement simple que lorsque l'observateur se trouve à l'équateur (cf. le point ci-dessous). En tout état de cause, ce facteur peut être négligé sans que cela ne modifie les résultats.

5) A l'équateur la réfraction et l'élevation ne jouent pratiquement aucun rôle sur l'azimut au lever du soleil. En effet on a $\mu_0=0$ et donc:

$\begin{displaymath} \cos \lambda = - \frac{\sin \Delta(j)}{\cos (\alpha_D + h_s)} \end{displaymath}$

(17)

Le dénominateur exprime le fait que lorsque $\Delta(j) \neq 0$ , le cercle décrit par le soleil sur la voûte céleste est une ligne d'égal $\theta'$ , mais donc ce n'est pas, pour l'observateur, une ligne d'égal $\lambda$ . Donc si on considère un point de la trajectoire du soleil qui est sous l'horizon, la valeur de $\lambda$ correspondant est très légèrement différente de celle obtenue lorsque le soleil est à l'horizontale. Ceci est illustré sur la figure suivante:

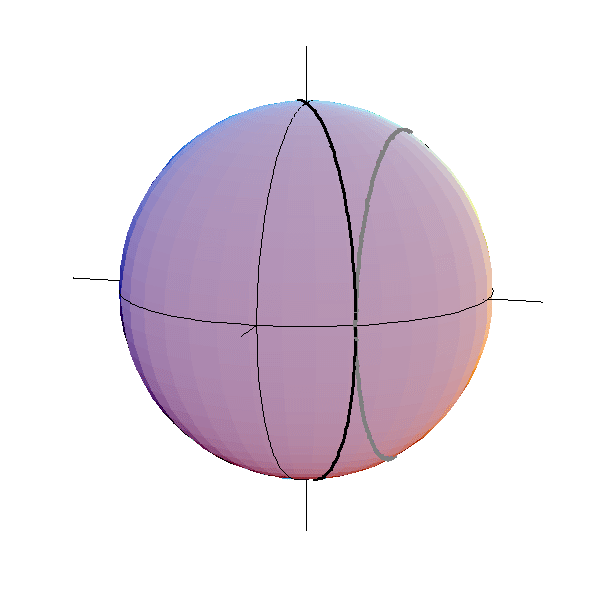
Sur cette figure, l'observateur est à l'équateur, et nous voyons de l'extérieur la sphère céleste telle qu'il la voit. La ligne de l'équateur céleste est la ligne noire fine verticale, et la ligne épaisse grise est la trajectoire du soleil ce jour-là, c'est donc un cercle d'égale $\theta'$ . La ligne épaisse noire est une ligne d'égal azimut (donc d'égal $\theta$ ) et puisqu'elle rencontre la trajectoire du soleil à l'horizon, l'azimut de cette ligne est donc l'azimut du soleil lorsqu'il se trouve à l'horizon. Maintenant, si l'observateur veut observer le soleil sous l'horizon (à cause de la réfraction), il faut qu'il se tourne légèrement. Cet effet est très faible car les angles de site en jeu sont eux-même très faibles. C'est pour cela que l'on peut sans danger négliger l'impact du facteur $\cos (\alpha_D + h_s)$ dans le dénominateur de la formule (15). Dans ce cas, l'azimut du soleil au lever à l'équateur est donné par:

6) Au pôle, l'impact de la réfraction est plus grand. La réfraction peut même "empêcher" le soleil de se coucher alors qu'astronomiquement il devrait le faire.

7) En plaine pour une latitude moyenne de +45 degrés environ, la réfraction déplace le lieu du lever (et du coucher) d'environ un diametre solaire vers le nord quel que soit le jour de l'année.

8) En montagne pour une latitude moyenne de +45 degrés environ, chaque tranche d'élevation de 800m environ déplace le lieu du lever d'environ un diamètre solaire vers le nord, et ce quel que soit le jour de l'année. Pour 2400m, on atteint donc un déplacement d'environ 3 diamètres solaires par rapport à un calcul purement astronomique.

9) Les deux effets (élévation et réfraction) étant assez faibles sur l'azimut, on peut considérer conceptuellement en première approximation qu'il s'additionnent simplement lorsqu'on les considère tous les deux. En effet puisque $\alpha_D$ et

sont des angles petits, on peut réécrire (15) comme suit:

$\begin{displaymath} \cos \lambda = - (\alpha_D + h_s) \tan \mu_0 - \frac{\sin \Delta(j)}{\cos \mu_0} \end{displaymath}$

(19)

Dans ce cas, le dernier terme donne la valeur "astronomique" de $\lambda$ , tandis que le premier terme du membre de droite donne la correction due à l'élevation (partie en $\alpha_D$ ) et à la réfraction (partie en

). Les deux corrections s'additionnent.

8 Azimut du soleil au lever, vu du Pic de Saint-Barthélemy

$\displaystyle z_0$	$\textstyle =$	$\displaystyle 2348m$	(20)
$\displaystyle \mu_0$	$\textstyle =$	$\displaystyle 42.82^\circ$	(21)
$\displaystyle \beta_0$	$\textstyle \approx$	$\displaystyle - 1.552^\circ$	(22)
$\displaystyle \alpha_D$	$\textstyle \approx$	$\displaystyle 1.703^\circ$	(23)
$\displaystyle h_s$	$\textstyle \approx$	$\displaystyle 0.56^\circ$	(24)

Pour une altitude d'observation de 2348 m l'erreur sur l'azimut au lever résultant de l'approximation de $\alpha_D$ est de l'ordre de 1/4 de diamètre solaire vers le sud, à comparer avec la correction de environ 4 diamètres solaires induite par l'élevation et la réfraction.