[ Accueil >
Faits et vérités sur le Pic >
Géodésie et altimétrie ]
Le massif de Tabe dans les mesures géodésiques et altimétriques
Mesures altimétriques pyrénéennes: une longue histoire
Jusqu'à l'avènement des techniques modernes, il a existé
essentiellement trois méthodes pour estimer la hauteur relative ou absolue
des montagnes.
Chronologiquement, la première de ces trois méthodes est le "pifomètre", méthode
qui a soivent prévalu jusqu'au 17eme siècle, et qui ne permet pas
une estimation quantitative absolue, mais simplement, et au mieux, un classement
hierarchique des montagnes en fonction de leur hauteur: "telle montagne est plus élevée
que telle autre". Au début, avant l'avènement de la méthode scientifique, et même
avant que les sommets ne soient eux-mêmes gravis, les résultats
sont largement fantaisistes. Chacun croit voir le point culminant de la chaîne
devant chez lui. Pour les catalans, il ne fait pas de doute que c'est le
Canigou qui marque le point culminant, pour les peuples de l'ouest (béarnais, gascons...),
c'est certainement
le Pic du Midi de Bigorre, pour les Touloulains et les couserannais, le Mont Valier,
et enfin pour les habitants de la partie Languedocienne des Pyrénées, c'est la
Montagne de Tabe: P. Olhagaray tient pour assuré en 1609 que "Tabe
est la plus haute montagne ès monts Pyrénées". Ajoutons que lorsqu'on l'applique
en gravissant les montagnes, cette méthode procure un avantage au sommet
qui est effectivement sous nos pieds: par exemple, vu du sommet du Pic de Saint-Barthélemy,
le Pic du Midi de Bigorre, bien que le surpassant de plus de 500 m, se retrouve
assez nettement au-dessous l'horizontale, à cause de la distance (133 km).
Il est donc assez facile, même avec la meilleure foi du monde,
de faire de grandes erreurs puisque les considérations
sur les effets de la rotondité de la Terre sont largement ignorés des
profanes qui utilisent la méthode.
La seconde méthode, qui permet en théorie
une mesure quantitative, est la méthode barométrique, inventée par Pascal.
Néanmoins, cette méthode souffre de nombreux inconvénients, et ne peut
prétendre avoir une valeur quantitative que si les caractéristiques générales
des variations verticales de la pression avec l'altitude sont connues, ce qui
est loin d'être le cas à l'époque de Pascal et de l'application de cette méthode
(au début du 18e siècle essentiellement).
Pour être capable de comprendre (et donc connaître) la variation verticale de
la pression avec l'altitude, il faudra attendre la fin du 18e siecle avec d'abord
les travaux sur la théorie des gaz parfaits (Mariotte) mais aussi et surtout ceux sur
l'équilibre hydrostatique de ces gaz (Laplace). En conséquence, cette méthode, qui
chronologiquement a été limitée à la période fin 17e - début 18e siècle,
a souffert d'une grande imprécision. Ajoutons aussi comme source d'erreur additionnelle
la variation dans le temps de la pression atmosphérique en chaque lieu, qui vient
sévèrement entacher d'erreur la détermination de l'altitude de référence,
étape primordiale pour cette méthode. Cette méthode à été notamment mise à l'honneur
par Maraldi en 1700-1703, et jusqu'à Monge qui l'utilisa en 1774, pour tenter
de mesurer le Pic du Midi de Bigorre. Maraldi (1703) reconnaît que cette méthode
quoique imprécise est très rapide, et permet donc une mesure indicative
précieuse pour mesurer les sommets dans des contrées mal connues ou très
éloignées de la mer.
La troisième méthode, celle qui fut appliquée à partir du 18e siècle est celle
que nous appelerons "géodésie", basée sur des visées, des mesures d'angles
et de longueur au sol. Cette méthode vise (si l'on peut dire!) en fait deux types d'objectifs légèrement
différents: le premier objectif était d'abord de déterminer la "forme de la Terre". Il faut entendre par là
déterminer la forme qu'aurait la Terre s'il n'y avaient pas les continents, ou
encore la forme de la Terre dans sa portion océanique. Ce premier objectif
est ce que l'on appelle "mesure du méridien"; ensuite le second objectif
était de déterminer la forme des irrégularités que représentent
les continents sur la Terre (altitude des montagnes , et cartographie, notamment),
une fois connue la forme de la Terre.
Paradoxalement, parmi les trois méthodes citées, c'est cette méthode "géodésique" qui tire
ses racines depuis l'époque la plus reculée, puisque Eratosthène, reprenant une idée
de Dicéarque en 300 av. J.C., l'utilise déjà pour mesurer le rayon de la Terre en 240 av. J.C.
Cette méthode, appliquée essentiellement dans des pays de plaine et qui
négligeait les aspects liés à la topographie fut continuée et précisée
par la suite, notamment par les arabes, puis les occidentaux à partir de
la Renaissance.
L'application de la géodésie au calcul de l'altitude des montagnes est plus récente:
c'est vers 1700 que l'on voit apparaître les premières
mesures d'altitude par la méthode géodésique, avec les observations
de Cassini et Maraldi (1700-1701), lors de la première campagne de mesure du méridien
de Paris sur toute la longueur du Royaume, de Dunkerque à Perpignan.
Une des motivations de ces mesures altimétrique était que le Canigou
mais aussi le Saint-Barthélemy avaient été qualifiés de sommet des
Pyrénées, et de France (voire même pour certains, d'Europe!).
Le pic de Saint-Barthélemy va donc faire à cette occasion partie
des trois premières montagnes à être mesurées. Ces trois montagnes sont
le Canigou, le Madres (baptisé Montagne de Mousset à l'époque), et le pic
de Saint-Barthélemy.
Le Pic de Saint-Barthélemy, l'une des toutes première montagnes au monde à avoir jamais été mesurées.
Le Canigou, le Madres, et le pic de Saint-Barthélemy ont toutes trois les même caractéristiques,
qui leur donneront l'honneur insigne d'être probablement les trois premières montagnes au monde a avoir été
mesurées scientifiquement, par la triangulation géodésique. Ces caractéristiques sont les suivantes:
- elles sont proches du méridien de Paris, objet principal des mesures;
- elles sont proches de la base mesurée (située dans la plaine du Roussillon), point
de référence pour toute mesure de distance et d'altitude;
- elles sont toutes trois visibles de l'extrémité de la base mesurée (dans le Roussillon).
Cassini et Maraldi souhaitaient mesurer le Canigou notamment parce que l'on pensait à cette
époque que c'était l'une des plus hautes montagnes des Pyrénées (et donc de France, ...
puisque la Savoie, où se trouvent les parties élevées des Alpes, ne
faisait pas partie du Royaume). Néanmoins, cette assertion sera infirmée dès 1726, par
de la Blottière, qui note que "les montagnes au dessus de Mont-Louis [...]
sont plus hautes que le Canigou".
Toujours est-il qu'une fois mesurée la base du Roussillon
et son élévation par rapport au niveau de la mer, les deux
savants ont pu attaquer directement la mesure des montagnes
visibles depuis cette base. C'est ainsi que nos trois montagnes
furent toisées les premières. Voici quelques courts extraits
du mémoire sur les mesures de Cassini, publié en 1718 (pp.11-112):
Le 18 Fevrier 1701, étant au Signal, qui eſt à l'extremité
Septentrionale de la meſure actuelle , dans un lieu élevé d'environ
9 pieds ſur la ſurface de la Mer, nous obſervâmes avec l'Octans ,
la hauteur apparente du Canigou ſur l'horizon artificiel de
2° 37' 0", celle du Mouſſet de 1° 44' 0", & la hauteur de la
Montagne de S. Barthelemi dans la Païs de Foix de 0° 50' 0".
Suppoſant le demi-diametre de la Terre de 3 271 420 toiſes,
tel qu'on le déterminera dans la ſuite, & la diſtance du Canigou
au Signal du Nord de 28 767 toiſes, celle du Mouſſet au Signal
du Nord de 35 145 toiſes , & la diſtance de S. Barthelemi
au Signal du Nord de 52 420 toiſes, telles qu'elles reſultent
des Triangles, on aura la hauteur du Canigou ſur le niveau
de la Mer de 1441 toiſes, celle du Mouſſet de 1253 toiſes,
& celle de S. Barthelemi de 1184 toiſes & demi.
L'ordre du mémoire n'est pas chronologique mais suit plutôt l'ordre
des calculs et de leurs résultats, que celui des observations.
La raison en est que par soucis de rigueur, les calculs se font
à rebours, une fois la base du Roussilon mesurée et connue.
Ainsi, un peu plus loin (p.120), ils mentionnent une nouvelle observation
du pic de Saint-Barthélemy effectuée depuis la ville de Puylaurens
(qu'ils écrivent Puy Laurent) dans le Tarn:
Le 5 décembre 1700, nous obſervâmes du haut de la
Tour de l'Egliſe de Puy Laurent , la hauteur apparente de
S. Barthelemy de 1° 2' 0" [...]. La diſtance du Puy-Laurent
à S. Barthelemy ayant été déterminée de 44 233 toiſes, [...] on aura la hauteur
de S. Barthelemy ſur le Puy Laurent de 1098 toiſes [...].
Ajoûtant à ces hauteurs celle du Puy-Laurent ſur le niveau
de la Mer qui a été déterminé de 97 toiſes, on aura la hauteur
de S. Barthelemy ſur le niveau de la mer de 1195 toiſes.
Enfin,juste après dans le cours l'ouvrage, ils mentionnent une observation
assez étonnante du pic de Saint-Barthélemy effectuée en même temps que celle
des monts du Cantal, ceci depuis un point unique qui est une hauteur
du Rouergue, près de Rodez :
Le 17 novembre 1700, nous obſervâmes de la Chapelle
de S. Jean, qui eſt ſur le ſommet de la Montagne de
Rupeyroux, la hauteur apparente du Plomb de Cantal dans
l'Auvergne de 0° 17' 10", celle du Puy-Mary de 0° 13' 0",
& celle du Puy de Violent de 0° 6' 15".
La hauteur de Rupeyroux ſur le niveau de la Mer ayant
été déterminée ci-deſſus de 407 toiſes & demie, & connoiſſant
la diſtance de Rupeyroux au Plomb de Cantal de 47 665 toiſes,
au Puy-Mary de 48 824 toiſes, & au Puy de Violent de 48 785
toiſes; on aura la hauteur du Plomb de Cantal ſur le niveau
de la Mer de 993 toiſes, celle du Puy-Mary de 956 toiſes, &
celle du Puy de Violent de 860 toiſes.
L'on voyoit de Rupeyroux, d'un côté vers le Nord les
Montagnes de l'Auvergne, & de l'autre vers le Midy, les
Montagnes des Pyrénées, quoi que la plus proche qui eſt
celle de S. Barthelemy, en ſoit éloignée de 87 740 toiſes.
Ces Montagnes, au lieu de paroître élevées ſur l'horizon ,
furent obſervées, à cauſe de la rondeur de la Terre, 13 à 14
minutes au deſſous de l'horizon artificiel, ce qui donneroit
la hauteur de S. Barthelemy encore plus grande qu'elle n'a
été déterminée par les obſervations précédentes.
En 1700-1701, Cassini et Maraldi avaient donc, pour les besoins de la
mesure du méridien de Paris, effectué les toute premières mesures
d'altitude des Pyrénées, et peut-être du monde, du moins avec une telle
rigueur et précision. Les mesures d'angles atteignent la demi-minute d'arc
(soit 30"). Pour le pic du Canigou, ils trouvent
une altitude de 1441 Toises, c'est à dire 2808 m (soit une erreur de +24 m).
Pour le Mousset (Madres), il trouvent 1253 toises c'est à dire 2442 m
(soit une erreur de -27 m), et pour le pic de Saint-Barthélemy, il trouvent
1184 et 1195 toises c'est à dire 2307 m et 2329 m (soit une erreur de -40 m et -19 m).
Pour l'époque cette précision de l'ordre d'une vingtaine de mètres est assez remarquable.
Remarques sur les mesures de Cassini:
Les mesures angulaires réalisées par cassini se révèlent généralement
d'une assez bonne exactitude pour l'époque, surtout en comparaison de
la médiocrité de certaines mesures ultérieures, comme celles de Reboul
en 1813 (cf. ci-dessous).
En revanche, la vérification des calculs de Cassini prouve que pour
ces trois premières mesures, il n'a été effectué aucune correction
pour tenir compte de la réfraction, ce qui finalement génère la
majeure partie des erreurs finalement obtenues sur les altitudes absolues
de ces trois montagnes lorsque toutes les mesures sont parfaites.
Le fait de négliger l'effet de la réfraction conduit à surestimer
l'altitude des montagnes, et ce, d'autant plus qu'elles
sont éloignées du point d'observation.
Pour le pic de Canigou la mesure angulaire (2° 37 ' 0") est à une demie-minute
près celle obtenues par le calcul moderne pour une atmosphère standard.
Comme c'est la précision atteinte par leur instrument, on peut donc dire
que leur mesure est parfaite. La distance indiquée (28767 toises = 56067 m)
est également parfaite puisque la distance réelle est de 56164m.
Cassini en déduit donc une altitude de 1441 toises = 2808 m trop
élevée (erreur de 24 m) , car il a négligé l'effet de la réfraction.
Pour le Madres, la mesure d'élevation angulaire est elle aussi parfaite,
mais la distance est sous estimée de 2 km, pour une raison inconnue
(68498 m au lieu de 70466 m), ce qui fait que finalement l'altitude
de la montagne se retrouve sous-estimée: 2422m au lieu de 2469 m
(erreur de -27 m).
Pour le pic de Saint-Barthélemy, la mesure angulaire indiquée est erronée
(0°50' au lieu de 0°55') Cette grosse erreur dans la mesure d'élevation
angulaire (ou dans sa transcription), se répercute sur l'altitude
finale calculée, qui est largement sous-estimée: 2308 m au lieu de 2348 m
(erreur de -40 m).
Finalement, étant donné les talents d'observateur de Cassini, le point
faible dans cette campagne semble être le manque de redondance dans les
mesures des sommets, une meilleure redondance dans les observations
aurait permis d'écarter les quelques mesures défectueuses, et d'obtenir
systématiquement une précision de l'ordre de la vingtaine de mètres.
Il est étonnant qu'une prise en compte même simplifiée des effets
de la réfraction n'ait pas été appliquée. Mais il faut dire que la
grandeur de ces effets étaient assez peu connue à l'époque. D'ailleurs
ce même mémoire consigne (entre autres) des mesures de bassesse de
l'horizon marin, observé depuis divers lieux, afin, sans doute de
progresser dans la compréhension des effets réfractifs et de pouvoir
ultérieurement les quantifier et en tenir compte dans les calculs
géodésiques.
Premier "Catalogue des hauteurs", et introduction de la méthode barométrique dans les Pyrénées
Les savants de la mesure de la méridienne du Royaume, Cassini et Maraldi
étaient parvenus à l'extrémité australe de leur périple dans l'hiver
1700-1701. Maraldi aurait désiré gravir les hauts sommets pyrénéens
afin de pouvoir "étalonner" la méthode barométrique, c'est à dire
qu'il aurait souhaité pouvoir mesurer expérimentalement la variation de
la pression avec l'altitude constatée (rappelons que la loi
de variation de la pression hydrostatique en fonction de l'altitude
n'était pas encore connue ou expliquée par la théorie).
Mais malheureusement (cf. Maraldi, 1703), la neige
hivernale l'empêcha de gravir ces sommets qui étaient pourtant
si proches:
[...]La hauteur du Canigou au-
deſſus de la ſurface de la mer meſurée en deux manières
différentes, a été trouvée de 1440 toiſes, qui font une peu
moins de trois quart de lieue de hauteur perpendiculai-
re. [...] Nous avions déterminé cette
hauteur, de même que celle de pluſieurs autres mon-
tagnes, dans le deſſein d'y faire l'expérience du Barome-
tre; mais nous n'avons pu l'exécuter à cauſe de la grande
quantité de neige qui les couvroit dans le tems de nos ob-
ſervations.
Comme la principale difficulté qu'il y a dans ces expé-
riences conſiſte à connoître la hauteur des lieux où on les
fait, nous avons cru devoir donner ici un Catalogue des
principales Montagnes, dont nous avons trouvé la hau-
teur ſur la ſurface de la Mer afin de donner occaſion aux
Sçavans qui ſe trouvent proches de ces Montagnes, d'y
faire l'expérience du Barometre, & voir ſi l'hypotheſe
que l'on propoſe répond à leurs observations.
|
Maraldi publie donc le catalogue des montagnes mesurées dans le Languedoc,
les Pyrénées et l'Auvergne, afin que ces hauteurs soient connues et
puissent être utilisées par ceux qui pourront les gravir, pour étalonner
la méthode barométrique. En fait de "Catalogue", c'est une liste
plutôt restreinte que nous livre Maraldi (voir ci-contre): en tout et pour
tout, onze sommets. Bien que cela ne soit jamais dit explicitement,
c'est bien en partie la recherche des points culminants des massifs
qui est l'une des motivations fortes de ces mesures. On remarque que
les erreurs sur les montagnes d'Auvergne, très éloignées de la base
du Roussillon sont très importantes (+121m pour le Puy de Sancy,
+107m pour le Mont Ventoux,...). En revanche, les trois montagnes
des Pyrénées, directement visibles du terme septentrionnal de la base,
sont affectées d'erreurs remarquablement faibles pour l'époque
(+23m pour le Canigou, -17m pour le Madres, et -20 m pour le
Saint-Barthélemy). Reboul dans 120 ans fera des erreurs bien pires (cf. ci-dessous)
|

| |
Extrait du mémoire de Maraldi (1703): catalogue des hauteurs mesurées pour les montagnes
du Languedoc, des Pyrénées et de l'Auvergne. Les explications du mémoire de Cassini
(1718) permettent de situer les montagnes cataloguées ici. Le "Puy Domme" est le Puy de Dôme,
la "Costa" est ???, le "Mont d'or" est le Puy de Sancy, etc.
(cliquer sur l'image pour l'agrandir)
|
|
Les Pyrénées et le Pic de Saint-Barthélemy, premières mesures barométriques par un pionnier intrépide: François de Plantade
Un peu plus tard, dans le premier tiers du XVIIIe siècle, l'astronome Montpellierain
François de Plantade fait de nombreuses expériences et observations
avec des baromètres, thermomètres et autres instruments, dans les montagnes de la partie
orientale des Pyrénéees. Il va gravir les trois sommets "proposés"
par Maraldi et un autre, intermédiaire. Ses observations semblent
répondre aux voeux exprimés par Maraldi (notons également que Plantade
était membre correspondant de l'Académie Royale de Sciences de Paris
comme l'attestent ses mémoires dans le domaine de l'astronomie).
|
Dans un mémoire lu devant la Société Royale des Sciences de Montpellier le
27 février 1732, il fait un résumé des diverses observations qu'il a
effectuées en 1731. Ce mémoire (Plantade, 1732) se trouve dans les
comptes rendus de l'Académie Royale des Sciences de Montpellier.
Par la méthode barométrique (et aussi géométrique
dit-il, sans toutefois en rapporter les calculs et les résultats),
il mesure quatre montagnes de la région:
- le "mont Ortiset" (l'actuel pic d'Ourtiset, ou d'Ourtisset selon les cartes, situé environ
à mi-chemin entre le Madres et le Saint-Barthélemy)
qu'il mesure à 992 toises (soit 1933 m, ce qui est d'ailleurs son altitude exacte)
- le "mont le plus oriental du Mousset", maintenant dénommé Madres (Le
Mousset étant un ancien nom de Mosset, la ville voisine), qu'il
estime, le 4 août 1731, à 1289 toises (2512 m, au lieu de 2469 m)
- le Canigou (1454 toises - 2833 m, au lieu de 2784 m), mesuré le 4 août 1731
- et enfin, le "mont St. Barthelemi"
qu'il mesure à 1190 toises (soit 2319 m, au lieu de 2348 m) le 25 août 1731.
Plantade affirme avoir
mesuré ainsi "plus de vingt montagnes", mais ne rapporte pas les résultats
de ces mesures. Il affirme également avoir vérifié géométriquement ces
mesures barométriques, dont celle du pic de Saint-Barthélemy, mais sans
donner aucun détail sur ce point.
|

|
Extrait du mémoire de F. de Plantade lu devant l'Académie des Sciences de Montpellier le 27 février 1732.
(cliquer sur l'image pour l'agrandir)
|
|
François de Plantade est un savant qui est exactement contemporain
de l'émergence de cette nouvelle science
appelée "histoire naturelle" et qui connaît un véritable essor à partir
du début du XVIIIe siècle. A cette époque, les mentalités se libèrent
à peine de l'esprit des XVIe et XVIIe siècle, si peu scientifiques, où
la parole des philospohes antiques vaut encore vérité intangible.
Dans ce mémoire, notre astronome aborde des questions scientifiques
pour le moins diverses et variées:
- l'eau bout elle spontanément sur les montagnes ?
- la vie des animaux et des êtres humains devient elle impossible sur les montagnes ?
- pourquoi les fleurs qui naissent sur les montagnes ont-elles des couleurs faibles ?
- est-il vrai qu'il y est nécessaire de respirer des "linges trempez dans des liqueurs spiritueuses" ?
- que le fer n'y rouille pas car l'air n'y a pas de "parties grossières, salines et corrosives" ?
- qu'en est-il au juste des légendes de des Etangs de tabe ?
- etc.
Si vous êtes intéressé par ces développements scientifiques parfois assez pittoresques,
voici la transcription du mémoire de François de Plantade
Ce naturaliste fait partie sans conteste de ces savants un peu explorateurs
dans l'âme et fort intrépides qui n'hésitent pas à quitter leur table
et leur plume, pour aller confronter leurs théories avec la réalité
du terrain, même s'il faut pour cela courir des risques. D'après ses dires,
Plantade aurait gravi une vingtaine de sommets pyrénéeens dans l'année
qui précède son mémoire. Plantade est le fondateur de l'observatoire
astronomique de Montpellier, et l'un des pionniers dans l'observation
scientifique au pid du Midi de Bigorre. Il mourra d'ailleurs sur les
pentes de cette montagne (au col de Sencours), le théodolite
à la main, lors d'une ultime campagne de mesures géodésiques.
Le Pic de Saint-Barthélemy, un point géodésique de "premier ordre"
Tout au long du XVIIIe siècle, les travaux de la "dynastie" Cassini se poursuivent,
à des fins de cartographie générale de la France. La triangulation "générale" de la France est
progressivement mise en place dans les zones habitées et facilement accessibles,
mais les cartographes s'arrêtent souvent dès les premières hauteurs,
le relevé des parties hautes et inhabitées étant considéré comme de peu intérêt.
Il faut dire que ce n'est que vers le milieu du XVIIIe siècle que les
montagnes en elles-mêmes deviennent peu à peu un sujet d'intérêt scientifique.
|
On peut voir ci-contre un extrait du relevé de triangulation établi
par Jacques Cassini en 1744. Quelques principaux pics, dont le
"pic de St-Barthelemi" sont signalés, et certains (comme le Pic
du Midi de Bigorre) sont utilisés à titre
de repère à longue distance, mais la partie montagneuse
ne fait pas réellement partie de la zone triangulée.
Dans cette carte, seuls une petite demi-douzaine de sommets sont
reportés pour l'ensemble de la chaîne, préfiguration du maillage principal qui sera adopté
une cinquantaine d'années plus tard par Reboul et Vidal, puis par Coraboeuf, et conservé
jusqu'à nos jours. Les cinq sommets portés sur cette carte de Cassini,
et qui obtiendront plus tard le statut de "point géodésique de premier ordre",
sont: le Pic d'Anie ("pic d'Anyon"), le Pic du Midi d'Ossau ("Montagne"),
le Pic du Midi de Bigorre ("Pic du Midy"), le Pic de Saint-Barthélemy
("St-Barthelemi") et le Pic de Canigou (absent de cet extrait).
D'après les indications de cette carte, il semble que le Pic de Saint-Barthélemy,
bien que répertorié, n'ait fait l'objet d'aucune mesure géodésique particulière
lors de la campagne de relevés ayant abouti à cette carte de triangulation de 1744.
En plaine, les repères utilisés par Cassini sont de nature variée, et parfois
un peu "risquée": à côté des églises de village, des moulins à vent ("Mn de Loupiac", Castillon,...)
et des sommets de collines ("St de Pech David", près de Toulouse,...), peu sujets
à disparaître, on trouve de nombreux points de repères pris sur des arbres
("Arbre d'Enramet", près de Lavaur, "A. de Montgrand", "A. de la Franquetat",...).
|

|
Extrait de la carte de triangulation établie par Jacques Cassini en 1744. Les Pyrénées
ne sont pas encore réellement comprises dans le territoire dont Cassini relève les mesures.
Une demi-douzaine de sommets remarquables de la chaîne sont tout de même reportés,
dont le Pic de St-Barthelemi en bas à droite.
(cliquer sur l'image pour l'agrandir)
|
|
Les premières mesures altimétriques visant à effectuer un
"nivellement général", c'est à dire une détermination de l'altitude de tous les
principaux sommets de la chaîne des Pyrénées, ne remontent qu'aux travaux du
géodésien H. Reboul, assisté de l'astronome J. Vidal, entre 1786 et 1789.
Cette première campagne fut complétée par ces deux mêmes scientifiques
une vingtaine d'années plus tard par une seconde, entre 1816 et 1817,
après que les soubresauts de la Révolution Française et des ses
conséquences se furent calmés. Il semble, d'après le contenu des écrits,
que pour la partie expérimentale, ce soit seulement Reboul qui est
allé faire les observations sur les sommets, le rôle de
l'astronome Vidal n'ayant été que de vérifier les calculs effectués
par Reboul une fois les observations terminées.
La méthode employée montre que le but de Reboul n'est pas de faire de la cartographie,
ce qui suppose la mise en place d'une triangulation géodésique précise et
méticuleuse dont ils se dispensent. Son but est plutôt de répondre à
quelques questions simples: quel est le point culminant du massif, et
quelles sont les altitudes des points les plus remarquables.
C'est d'ailleurs Reboul qui le premier pressent que le point culminant de la
chaîne est le pic d'Aneto, mais sans pouvoir l'établir formellement,
notamment à cause des trop fortes incertitudes de mesures (cf. infra).
Dès ces premières mesures altimétriques couvrant l'ensemble de la chaîne,
le Pic de Saint-Barthélemy fait partie de la liste des dix points de station
choisis tout au long de la chaîne pour observer l'ensemble des autres sommets.
Les dix points de stations choisis par Reboul sont:
- le Pic dAnie, stationné en 1786
- le Pic de Midi de Bigorre, stationné en 1786 et 1787
- le Couroua ou Bergons, stationné le 1er août 1787
- le Neige-Vieille-Cap-Longue, stationné en août 1787
- le pic d'Arré dans la vallée d'Auze, stationné le 25 juillet 1789
- le pic d'Irré dans la vallée de Gistain , stationné les 29 juillet 1789
- le pic Crabère dans la vallée de Melles, stationné en 1789
- le sommet de Pouëylouvic à l'origine de la vallée de l'Arboust, stationné le 14 août 1816
- la serre de St Paul entre les vallées d'Oüeil et de Luchon, stationné le 7 septembre 1816
- en enfin le pic d'Appi-St.-Barthélemi, stationné le 9 septembre 1789.
|
|
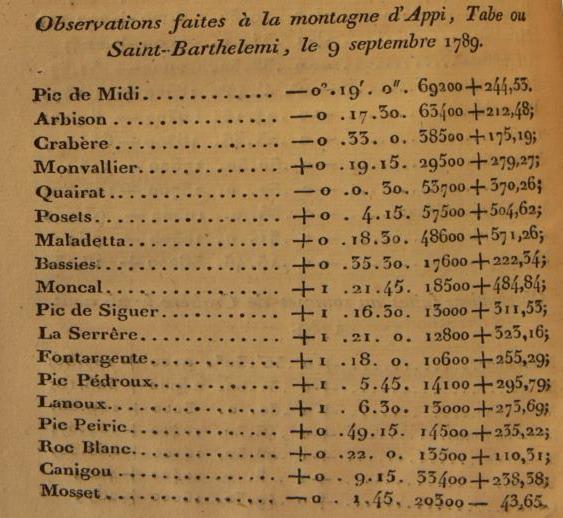
Extrait du mémoire de Reboul (1817), page. 12.
Tableau des dix-huit sommets visés le 9 septembre 1789 depuis le pic de saint-Barthélemy
par Reboul.
(cliquer sur l'image pour l'agrandir)
|
|
Du Pic de Saint-Barthélemy, Reboul vise un grand nombre de points (dix-huit exactement), allant du Canigou
au Pic du Midi de Bigorre, et embrassant donc une distance d'environ 200 km d'un seul
coup d'oeil. Le tableau ci-contre montre les résultats obtenus grâce à ces mesures.
La première colonne est l'angle d'élévation du point visé par rapport à l'horizontale, la
seconde est la distance en toises (mesurée sur la carte de cassini),
et la dernière est la différence d'altitude (en toise) qui s'en déduit,
en tenant compte d'une manière simplifiée de la courbure
de la Terre et de la réfraction atmosphérique. Noter que le
sommet baptisé "Mosset" est en réalité le Madrès dans la nomenclature
actuelle.
|
Reboul et Vidal se sont donc bornés à mesurer les altitudes des sommets
les plus remarquables, en relevant simplement leurs distances sur la carte de Cassini, détail
curieux lorsque l'on sait le peu d'exactitude des cartes de l'époque, à laquelle
celle de cassini n'échappe pas. La plupart du temps donc, ils ne font pas de
triangulation géodésique, sauf pour les sommets espagnols, qui ne sont pas
inclus dans la carte de Cassini, et dont il faut alors mesurer la distance
directement par triangulation. En définitive, on peut dire que les résultats
obtenus par Reboul sont assez mauvais pour l'époque, et les altitudes obtenues
ont des erreurs environ 20 fois trop forte par rapport à ce que l'on aurait
pu attendre vu la précision des instruments de l'époque. Les erreurs vont
jusqu'à 60 m, alors qu'une méthodologie plus rigoureuse aurait probablement
permis d'atteindre une précision d'environ 3 mètres dès cette époque.
Curieusement, ce ne sont pas les erreurs liées à l'utilisation de ces cartes
anciennes qui vont finalement peser le plus lourd dans les erreurs
totales, mais tout simplement des erreurs énormes dans les visées effectuées
par Reboul: on note des erreurs de visée allant jusqu'à 9 minutes
d'arc (le tiers du diamètre lunaire !) alors que la précision qu'on
peut attendre couramment à cette époque est d'1/4 de minute d'arc
(15" d'arc). Il est difficile de savoir d'où peuvent venir ces erreurs de visée,
mais il faut probabalement y voir un défaut du calage d'horizontalité de l'instrument
et un protocole de mesure défectueux (notamment, il n'y a pas de répétition
des mesures effectuée de façon indépendante, ce qui aurait permis de détecter
les erreurs de calage horizontal).
Voici, pour la seule station du pic de Saint-Barthélemy, la liste de quelques visées, avec les résultats
et les erreurs commises par Reboul:
Sommet
visé |
distance (*) |
angle
d'élévation |
erreur sur
l'angle
d'élévation |
diférence d'altitude
conclue |
erreur sur la
diférence d'altitude
conclue |
| Pic de Midi |
133.0 km |
-0°19'0" |
+1'34" |
+476.6 m |
+52.4 m |
| Mosset |
39.2 km |
-0°1'45" |
-3'15" |
+85 m (**) |
-36 m |
| Canigou |
65.3 km |
+0°9'15" |
+1'22" |
+464.6 m |
+28.6 m |
| Pic Pédroux |
27.0 km |
+1°5'45" |
+9'5" |
+576.5 m |
+82.5 m |
| Monvallier |
56.0 km |
+0°19'15" |
+2'9" |
+544.4 m |
+54.4 m |
| Roc Blanc |
25.4 km |
+0°22'0" |
+1'34" |
+215.0 m |
+21.0 m |
(*) nous donnons ici les distances réelles, et non celles portées par Reboul dans sa Table
(**) après correction d'une erreur de signe visible dans la dernière ligne de la photo
ci-dessus reproduisant la Table donnée par Reboul.
Les résultats des mesures de Reboul et Vidal furent publiés dans la revue "Annales
de Chimie et de Physique", Paris (1817), mais également auparavant
dans l'ouvrage de E. Dralet "Description des Pyrénées" (1813); ils sont
également cités par plusieurs auteurs,
notamment Chausenque (1834, rééd. 2006).
|
Pour le Pic de Saint-Barthélemy, Reboul a déterminé une élévation de 1192 toises (2322.5 m)
par les mesures effectuées le 9 septembre 1789 "à la Montagne d'Appi,
Tabe, ou St-Barthélemi", et au "sommet de Crabère". L'erreur est donc
de 25 mètres environ, ce qui est un résultat tout à fait moyen
(Cassini et Maraldi avaient fait mieux 120 ans plus tôt, sans
que cela représente une coïncidence spécialement heureuse).
Le statut de "point remarquable" dont a joui dès le début notre
Pic de Saint-Barthélemy, fut ensuite toujours conservé, et les géodésiens à venir
lui attribuèrent dès l'origine le statut de "point géodésique de premier ordre",
ce qui fait qu'il a ensuite été toisé à chaque nouvelle campagne de mesure.
C'est ce qui explique donc que notre pic soit l'une des cinq ou six montagnes
qui ont été le plus toisées dans tout le massif (c'est d'ailleurs la seule à
posséder trois mesures dans la liste publiée par Chausenque).
|

|
Extrait du mémoire de Reboul (1817), mentionnant les résultats pour l'altimétrie
du pic de Saint-Barthélemy.
Première ligne: observation du Saint-Barthélemy
à partir de la station du Crabère. Lignes suivantes visées effectuées
à partir du Saint-Barthélemy vers des montagnes déjà connues:
le Crabère, le Vallier, le Quairat, et la Maladetta. Le résultat moyen est 1192 toises, soit 2322.5 m.
(cliquer sur l'image pour l'agrandir)
|
|
Le Pic de Saint-Barthélemy: son rôle dans la triangulation complète et la cartographie de la chaîne
La première campagne de relevés en vue d'une triangulation complète de la chaîne des Pyrénées,
dans ses moindres détails, non plus pour les simples besoins des mesures
de hauteur, mais pour ceux bien plus complets de la cartographie
d'Etat Major, eut lieu entre 1825
et 1827 par une équipe d'officiers géodésiens. Sous les ordre du Lieutenant-Colonel
Coraboeuf, le capitaine Peytier et les lieutenants Testu et Hossard
menèrent à bien ces opérations géodésiques, d'une mer à l'autre.
Quarante points de premier ordre furent mesurés, en longitude, latitude, et altitude,
avec le plus grand soin et la plus grande précision. Ces points permettaient
d'établir deux chaînes de triangles, l'une australe, près de la crête
frontière, l'autre boréale sur des sommets plus en avant, ces deux chaînes
servant à vérifier et consolider les résultats obtenus.
Les observateurs Peytier et Hossard furent chargés de la partie ouest de la chaîne,
de l'océan jusqu'aux pic de Crabère et Maupas,
tandis que Corabeuf et Testu s'attribuèrent la partie est, de la Méditérranée
jusqu'à ces mêmes pics.

|
Extrait de la page 216 du tome I de Beraldi : "Cent ans aux Pyrénées" (1922).
Cet ouvrage retrace, entre autre, l'épopée des officiers géodésiens lors
de cette campagne de nivellement général des Pyrénées.
(cliquer sur l'image pour l'agrandir)
|
|
Campant le plus souvent au sommet même des points de stations,
les géodésiens eurent fort à faire avec les éléments, qui bien
souvent ne leurs étaient pas favorables.
Coraboeuf et Testu atteignirent le Pic de Saint-Barthélemy
en septembre 1826, comme le relate Beraldi dans "Cent ans aux Pyrénées" (1922),
dont l'extrait en question est reproduit ci-contre.
Les mesures étaient très minutieuses et demandaient plusieurs heures d'affilée
d'une météo clémente et d'une bonne visibilité. Sur certains
points de station, il fallut rester une quinzaine de jours avant
de pouvoir compléter le programme d'observations (par exemple sur le Canigou,
selon l'extrait ci-contre).
|
Les relevés des géodésiens Coraboeuf et Testu, lors de cette campagne de 1825-1827,
ont permis d'attribuer au "Pic de Saint-Barthélemi, signal de
premier ordre", la hauteur de 2348.8m, et la carte d'Etat Major
au 1/80000 a donc adopté la côte 2349m, et ceci, pour une centaine d'année
(l'altitude officielle du pic est maintenant de 2348 m).
Au cours de cette campagne initiale de 1825-1827, les officiers géodésiens
mesurèrent très précisément les coordonnées et altitudes des quarante
points de premier ordre, sur lesquels ils stationnaient
parfois jusqu'à deux semaines.
Mais à cette tâche de nivellement du premier ordre, il ajoutèrent
le nivellement de 122 points de second ordre, par visée et
triangulation. Ils ne gravirent donc pas physiquement les sommets
correspondant à ces points de second ordre.
Plus tard, des milliers de points de troisième ordre seront mesurés
lors de campagnes de relevé entre 1848 et 1851 par des légions de topographes
afin de pouvoir entamer enfin la cartographie des Pyrénées, ce qui
aboutira à la carte d'Etat Major au 1/80000e, dont la pulication de la
première édition s'étalera entre 18?? et 18?? selon les régions.
Pour les Pyrénées, les cartes seront disponibles vers 18??.
Voir sur le site de Gallica, le mémoire de Coraboeuf ,
publié en 1832 dans les
"Mémoires présentés par divers savans à l'Académie Royale des Sciences de l'Institut de France" (1832, T.3, pp. 45 - 132).
Voir aussi:
- Corabeuf : Description de la chaîne des
Pyrénées Mémorial du Dépôt de la Guerre, Tome VI, pp. 334-361,
Paris, 1832
- Corabeuf : Opérations géodésiques des
Pyrénées et la comparaison du niveau des deux mers.
Mémorial du Dépôt de la Guerre, Tome VI, pp. 361-403,
Paris, 1832
N.B.: Ces deux monographies sont rarissimes et ne peuvent être
consultées qu'à Paris, pour ce qui est des bibilothèques publiques.
On peut toutefois trouver une courte synthèse des résultats de Corabeuf
(ainsi que le rappel des mesures de Reboul et quelques autres
prédecesseurs) à la fin de l'ouvrage de Chausenque (1834, rééd. 2006).
Le Pic de Saint-Barthélemy: son rôle dans la "mesure du monde"
Ensuite, il faut savoir que le Pic de Saint-Barthélemy a reçu
l'insigne honneur de faire partie de la petite centaine de points
remarquables choisi de part
et d'autre du "méridien de l'Observatoire" pour "la mesure du monde",
comme disaient les révolutionnaires.
De quoi s'agit-il ? Les Etats Généraux de 1789 avaient massivement
formulé comme doléance qu'en France, on n'usât qu'un seul poids
et une seule mesure, en remplacement des
quelques 2000 unités locales en usage à travers tout le royaume à cette époque.
Sur proposition de la Commision des Poids et Mesures créée à cet effet,
il fut décidé par l'Assemblée que l'unité de longueur serait la 40 millionième
partie du méridien terrestre, ce qui devait donner à cette nouvelle unité
(qui n'avait pas encore reçu de nom) la longueur d'environ une demi-toise
du Pérou. Mais pour cela, il fallait bien mesurer la longueur du méridien
terrestre. Grace aux progrès récents de la technique, une méthode par
triangulation pouvait, au prix de longs et fastidieux calculs géométriques,
offrir une précision suffisante pour cette mesure,
à condition de connaître la longueur exacte de l'une des bases de l'un des
triangles. C'est cette entreprise gigantesque d'arpentage de la Terre
pour connaître la longueur du méridien qui nous amène
au voisinage du Pic de Saint-Barthélemy, puisque le méridien qui fut choisi
était le méridien reliant le coq de la Tour de Dunkerque au Fort de Montjouy (Monjuich),
près de Barcelone, et passant dans la ville de Paris. En fait, la commission chargea
deux astronomes (Delambre et Méchain) de mesurer seulement la portion
du méridien comprise entre Dunkerque et Montjouy .
Les latitudes de ces deux lieux étant mesurées avec précision, cela suffisait,
moyennant certaines hypothèses sur la forme générale de notre globe, à
connaître ensuite la longueur totale du méridien.
Delambre fut chargé de la partie nord du parcours (Dunkerque-Rodez), et Méchain
de la partie sud (Montjouy-Rodez). Les péripéties de cette aventure sont relatées
avec force détails dans le roman de Denis Guedj, "La Méridienne", 1997,
Ed. Robert Laffont. Voir aussi l'ouvrage "Le Mètre du Monde" du même auteur
Ed. Le Seuil. Cette gigantesque aventure,
ralentie par les vicissitudes de l'Histoire durant cette période tourmentée
a duré sept années, de 1792 à 1799.
Le principe de la mesure géodésique est de calculer les angles que
forment entre eux les points choisis. Chaque point est alors à la fois
un point observé, puis un point d'observation. Pour cela, les points
d'observation étaient pourvus d'un "signal" qui permettait de localiser
avec précision l'emplacement de l'instrument de mesure.
Mais dans la partie la plus montagneuse, il y avait une seconde sorte de
points observés, qui consistaient en des points visibles de très loin
et sur lesquels Méchain n'est pas allé physiquement pour faire des mesure.
Ces points remarquables servaient à titre de vérification sur des longues
distances. Ces points ne sont donc pas classés dans la catégorie "signal".
|
Le Pech de Bugarach situé presque exactement sur le méridien
mesuré, était un signal, c'est à dire que Méchain a dû se hisser en
son sommet avec son matériel. Ce signal fut un haut lieu de l'aventure
(où les instruments de mesure de Méchain faillirent finir fracassés
au fond d'un ravin). En revanche, le Pic de Canigou et
le Pic de Saint-Barthélemy, ne furent pas des signaux, et donc ne furent
pas gravis par l'astronome, mais seulement visés, sur de longues distances.
Delambre a consigné intégralement les résultats de ces mesures dans un livre
qu'il publia entre 1806 et 1810 "Base du Système Métrique Décimal".
Comme on peut le voir sur la figure ci-contre, le "Mt St-Barthélemy" a été
visé depuis les signaux de Carcassonne et de Bugarach .
|

|
Extrait de la page 557 du tome I livre de Delambre (1810), représentant les visées dans la région
du Massif de Saint-Barthélemy
(cliquer sur l'image pour l'agrandir)
|
|

|
Extrait de la page 380 du tome I livre de Delambre (1810): distance zénithale
du mont St Barthélemy vu depuis le signal de Bugarach
(cliquer sur l'image pour l'agrandir)
|

|
Extrait de la page 382 du tome I livre de Delambre (1810):
azimut entre le mont St Barthélemy et le signal de Carcassonne,
vu depuis le signal de Bugarach
(cliquer sur l'image pour l'agrandir)
|
|
Le "Mont Saint-Barthélemy" a d'abord été observé depuis le Pic de Bugarach
le 5 et 9 brumaire an 4. On apprend qu'en fait c'est le
"Pic de Lestangtost du Mont Saint-Barthélemy" qui fut visé. Cette dénomination
est expliquée en détail un peu plus loin dans le texte: il s'agit du "pic oriental, le plus
haut du Mont St-Barthélemy", c'est à dire
le Pic de Soularac dans notre terminologie moderne. Noter que ce nom "Pic de Lestangtost"
correspond en fait à "Pic de l'Etang Tort", du nom de l'étang en forme de
haricot qui est situé dans le flanc est du Pic de Soularac.
L'auteur indique que "on visoit à un petit mamelon, très-remarquable sur le pic de Lestangtost".
Il s'agit en fait du rocher sommital, qui coiffe le pic. Sur les pages reproduites ci-contre,
c'est les observations relatives à la distance zénithale du Mont St-Barthélemy (Fig. du haut)
puis à la différence d'azimut
entre le signal de Carcassonne et le mont Saint-Barthélemy (Fig. du bas), le tout
observé depuis le signal de Bugarach, qui sont consignées.
|
|
Ensuite, Méchain s'est transporté de Bugarach à Carcassonne pour poursuivre
ses mesures en direction du Nord. Le "Mont Saint-Barthélemy" a été observé depuis
le signal de Carcassonne (situé au sommet de la Tour Saint-Vincent)
le 27 brumaire an 4.
Sur les pages reproduites ci-contre,
c'est les observations relatives à la distance zénithale du Mont St-Barthélemy (Fig. du haut)
puis à la différence d'azimut
entre le signal de Bugarach et le mont Saint-Barthélemy (Fig. du bas), le tout
observé depuis le signal de Carcassonne, qui sont consignées.
|

|
Extrait de la page 373 du tome I livre de Delambre (1810):
distance zénithale du Mt St Barthélemy vu depuis le signal
de Carcassonne
(cliquer sur l'image pour l'agrandir)
|

|
Extrait de la page 376 du tome I livre de Delambre (1810):azimut entre le Mt St Barthélemy et
le signal de Bugarach, vu depuis le signal de Carcassonne
(cliquer sur l'image pour l'agrandir)
|
|
L'énigme de la hiérarchie inversée entre Soularac et Saint-Barthélemy
Détail insolite, pratiquement dès l'origine des mesures et pendant très longtemps,
le Pic de Soularac fut gratifié d'un simple 2343 m, c'est à dire 6 mètres de moins
que le Pic de Saint-Barthélemy (qui lui était pointé à 2349 m). Rappelons que le
Soularac domine en réalité le pic de Saint-Barthélemy de 20 mètres, du haut de ses 2368 m.
Cette inversion de hiérarchie, qui semble s'être
étalée sur plus d'un siècle (entre 1826 et 1939 environ) résute d'une erreur
manifeste car du sommet de l'un des deux pics (distants seulement de 800 m à
vol d'oiseau) la véritable hiérarchie est assez évidente.
Néanmoins, une fois l'erreur commise, il faut admettre que la crédulité
et le respect des "savants" a pu contribuer à l'accepter comme vérité, ou
comme une étrange illusion d'optique: puisque les savants
le disaient...cela devait être vrai.
Cette erreur apparaît non seulement sur toutes les cartes, mais également dans
tous les écrits de l'époque.
Une mesure initiale erronée ? La réponse est définitivement
NON. Les mesures effectuées par Coraboeuf sont parfaitement correctes, car elles
mentionnent 2349 m pour le Saint-Barthélemy et 2369 m pour le Pic de... Lestangtot.
Ce sommet, qui n'est autre que le pic de Soularac, est un point de second
ordre, qui a été visé à partir de cinq stations : le Pech de Bugarach,
le Madres, le pic oriental de Col-Rouge, le Montcalm, et le Tuc de la Courate.
Dans la table récapitulative des altitudes des sommets du second ordre, le pic
est répertorié sous la dénomination "Pic de Lestangtot. - St Barthélemi".
Ce nom de Pic de Lestangtot mérite que l'on s'y arrête. Il correspond
au nom du pic qui avait été choisi comme repère par Méchain: "Pic de Lestangtot, ou
Pic oriental et point culminant du Mont Saint-Barthélemy". Ce pic, qui domine
directement l'Estang Tort, est sans équivoque l'actuel pic de Soularac, d'autant
plus que les mesures d'azimut de Méchain permettent de situer exactement
ce pic de Lestangtot comme étant le Soularac. Si on cherche encore une preuve supplémentaire,
Méchain "vise au mamelon très-caractéristique qui est au sommet", et qui est
le rocher sommital du Soularac que l'on peut encore y voir de nos jours.
On voit donc qu'au cours des deux campagnes (Méchain et Coraboeuf), le pic
de Soularac est affublé d'un nom plus ou moins fantaisiste et peu usité
(on relèvera aussi "pic de Lestanglot" dans Chausenque, 1834, et même des
"pic de Stantor", puis "Stentor" dans certaines sources de ces époques!).
Donc, dans les relevés de Coraboeuf, le bon pic (Soularac) est affecté de la
l'altitude correcte (2369 m), mais sous un nom (Lestangtot) prêtant à
confusion. Finalement, détail pittoresque, il est plaisant de s'imaginer
que la source ultime cette erreur d'un siècle vient peut-être de l'utilisation
d'un toponyme dont l'usage était déjà trop local ou trop peu
usité pour rester facilement localisable par la suite.
A qui la faute ? L'ensemble des résultats relevés par nos géodésiens
au cours de leurs campagnes pyrénéennes furent ensuite regroupés et synthétisés
en un mémoire. C'est sur ce mémoire que l'on voit figurer les relevés du
pic de Saint-Barthélemy à 2349 m, et ceux concernant
l'énigmatique pic de Lestangtot à 2369 m. L'étape suivante était de reporter
sur le fond de carte ces pointages altimétriques, ainsi que les indications toponymiques
correspondantes, relevées, elles-aussi sur le terrain (mais séparément, au cours
de campagnes de collectes spécifiques).
A partir de là, le terrain ne joue plus aucun rôle, et le travail s'effectue
bien au chaud, à la table.
C'est sous la direction du Colonel Puissant que s'effectue cette tâche qui
consiste à porter les noms et les altitudes correspondantes sur le fond de carte.
Apparemment, c'est à cette étape que s'est produit l'erreur qui perdura
plus de cent ans, en dépit de toutes les évidences.
Tentative d'explication (dans ce paragraphe, il s'agit d'une
explication personnelle, très plausible, mais non prouvée).
Pour notre pic de Soularac, les cartographes en salle qui se chargent
des étapes suivantes se heurtent à un
problème: ils ont d'un côté le toponyme "pic de Soularac" bien connu,
qu'ils savent parfaitement devoir placer
à 800 m à l'est du Pic de Saint-Barthélemy, mais au moment d'en consulter
l'altitude dans le mémoire des géodésiens, ce pic reste introuvable dans les
tableaux. D'un autre côté, il y a un relevé relatif à un certain
"pic de Lestangtot, côté à 2369 m, mais à ce stade des opérations, plus
personne ne sait où se situe ce mystérieux pic, par ailleurs pas assez
elevé pour qu'on s'y attarde outre mesure: encore s'il s'était agit d'un "3000"!.
Les cartographes en salle
ne parviennent pas à faire le rapprochement entre le pic en trop dans le
relevé altimétrique, et l'absence de mesure correspondant au pic de Soularac.
Oui, mais alors pourquoi ce 2343 m pour le Soularac ?
(dans ce paragraphe, il s'agit encore d'une
explication personnelle, très plausible, mais non prouvée).
Lorsque plusieurs mois ou années après les campagnes de terrain, il a fallu
affecter sur la carte une altitude au pic de Soularac, il n'était plus
question de dépêcher spécialement une nouvelle mission à cette fin.
L'hypothèse la plus plausible est qu'alors on se soit contenté de
prendre pour le Soularac l'altitude la plus réaliste qu'on eût sous la
main, et que celle-ci soit celle relevée par Reboul une quarantaine d'années
auparavant (en 1789). En effet, Reboul ayant trouvé 2323 m pour le Saint-Barthélemy,
il est évident qu'il n'a pas pu s'empêcher de toiser son voisin (et aîné) immédiat
et de lui trouver, en comparaison, 2343 m: la mesure de l'un connaissant l'autre
est en effet quasi-immédiate, étant donné la proximité des deux sommets.
On a beau remuer les chiffres dans tous les sens, à la date de 1827, il n'y
a aucun autre moyen d'expliquer raisonnablement cette altitude fantaisiste:
en 1827, les progrès de la géodésie par rapport à 1789 étaient tels qu'une
erreur de 25 m sur une mesure de l'altitude du Soularac, si aisément
accessible et visible de partout y compris en plaine, est inimaginable.
L'altitude de 2343 m officiellement adoptée ne peut résulter, à cette date
que d'une absence de mesure.
Durée de l'erreur: L'erreur s'étale sur une durée de plus d'un
siècle. Dès la première carte "moderne" (c.à.d. où les altitudes sont pointées),
l'erreur est présente. Cette première carte est la carte de l'Etat-Major,
en 267 feuilles, levée au 1:40000e et gravée au 1:80000e, et qui utilise
pour l'altimétrie les données issues des mesures de Coraboeuf.
La première édition de cette carte semble remonter à 1850
(pour cette feuille), et on y relève la mention: pic de Soularac 2343 m.
Un demi-siècle plus tard, l'édition de 1898, d'ailleurs très peu différente,
comporte toujours l'erreur.
En 1930, l'erreur remonte à une centaine d'année, malgré la révision générale
de 1900, et se trouve toujours sur la nouvelle carte au 1:50000e.
Il reste à retrouver des cartes côtées datant des années 1940 pour pouvoir
dater plus précisément la fin de cette inversion.
Ceux qui acceptent l'erreur: Comme indiqué ci-dessus, il n'est pas facile
lorsque l'on est simple chroniqueur, de contester en vertu de l'évidence,
le travail et les résultats des "savants", les géodésiens qui ont tranché
pour cette vérité scientifique implacable: pic de Soularac 2343 m.
Alors, on accepte, et on met probablement sur le compte d'un effet
d'optique (ou de quelque phénomène naturel merveilleux coutumier de la région)
cette impression visuelle que le Soularac domine le Saint-Barthélemy.
Voici quelques témoignages de l'époque:
- Géographie de l'Ariège Adolphe Joanne, 1880, Ed. Hachette (p.5): Montagne de Tabe [...]
Après s'étre abaissée, elle se relève au Pic de Soularac (2343 m); elle se continue par
le Pic de Saint-Barthélemy (2349 m).
- Le massif de Tabe, Hippolyte Marcailhou d'Aymeric, 1898. L'altitude erronée
"pic de Soularac, 2343 m" apparaît à de multiples reprises, tout au long de cette monographie.
- Ax-les-Thermes, Guide du Touriste et de l'Alpiniste, Brochure éditée en 1925
(3e édition, la première datant de 1906)
par le Syndicat d'Initiative d'Ax-les-Thermes (pp. 17-18): Ascension au Pic de saint-Barthélemy. [...]
Le sommet couronné par un amas de pierres,
débris d'un ancien oratoire dédié à Saint-Barthélemy est le pont culminant du massif de
Tabe (2349 m). [et un peu plus loin] Ascension au Pic de soularac (2343 m) [...]
Vue très belle mais un peu moins étendue, surtout au nord-ouest que celle de son
rival et voisin le pic de Saint-Barthélemy (2349 m) à peine plus élevé que le
Soularac et séparé de lui par l'échancrure du Pas de l'Ours
- La région pyrénéenne de notre France, sa géographie son Histoire, P Arqué et Ch. Dartigue-Peyrou, 1948,
Ed. Charles Lavauzelle, (pp. 10 et 11): le Saint-Barthélemy (2349 m) est désigné comme sommet
du massif (l'erreur sur le Soularac n'est toutefois pas mentionnée explicitement).
- A compléter
Les quelques voix qui refusent l'erreur: Après des années d'acceptation,
on voit apparaître timidement quelques voix qui doutent.
-Pyrénées Ariégeoises - Livret-Guide, brochure éditée par le Syndicat d'Initiatives
de l'Ariège en 1918 (p. 7): Pics de Saint-Barthélemy (2349 m) et Soularac (2360 m)
points culminants du Massif de Tabe.
-A compléter
L'origine exacte de l'indication 2360 m reste une énigme (probablement une estimation
grossière à vue de nez).
Rétablissement de la hiérarchie: Il est possible (mais cela
demande vérification) que la véritable hiérarchie
n'ait été rétablie officiellement qu'en 1939, lors d'une mission spécialement
dépêchée, enfin dédiée à cette question. Ceci expliquerait le vestige portant
cette date au sommet du pic de Saint-Barthélemy (voir ci-dessous).
épilogue citation rectifiant l'erreur récemment corrigée.
-Les Cathares de Montségur, Fernand Niel, 1973, Ed. Robert Laffont (pp. 37 et 303): Les deux
pics jumeaux du Soularac et du Saint-Barthélemy sont distants d'à peu près huit cents mètres (...)
Ils ont à peu près la même altitude, 2368 m pour le premier, 2348 m pour le second. Ces altitudes
sont celles portées sur les nouvelles cartes de l'Institut Géographique National. Elles redressent
une erreur acceptée pendant longtemps, due aux anciennes cartes d'état-major, qui indiquaient les
altitudes de 2349 m pour le St-Barthélemy et 2343 m pour le Soularac.
-A compléter
La saga du "sommet de la France"
Longtemps, l'emplacement du point culminant du Royaume de France est resté ignoré.
On l'a vu, pour Pierre Olhagaray (1609) historiographe du roy de France Henri IV,
il ne fait pas de doute que "Tabe ou Tabor est la plus haute montagne ès monts Pyrénées",
et donc ainsi à cette époque, c'est notre pic de Saint-Barthélemy qui officiellemment
représente le point culminant de la France, puisque les Alpes sont réputées moins hautes
que le Pyrénées (cela est sans doute dû au fait que la partie alpine du Royaume de
France ne contient pas la Savoie, qui ne sera réunie que bien plus tard, au XIXe
siècle). Néanmoins, il ne faut pas oublier les remarques du début de cette page,
selon lesquelles, par l'effet de l'optique chacun voit le point culminant à sa
porte...
Olhagaray était né et a passé la majeure partie de sa vie dans la ville de
Mazères, entre Pamiers et Mirepoix, précisément dans la région où, optiquement,
le pic de Saint-Barthélemy domine, et de loin, tous les autres sommets. D'ailleurs,
selon certains étymologistes modernes (Durand, Taillefer), Mirepoix tire sa dénomination non pas de
"mira pisces", mais de "mirum podium", c'est à dire "admire la montagne".
Il n'y a donc rien d'étonnant à ce qu'Olhagaray se laisse prendre à l'illusion
et clame son affirmation sans appel.
Mais cette affirmation, bien que jamais contredite formellement semble
n'avoir jamais eu un crédit très partagé. En fait, c'est le Pic de Canigou
qui a joui pendant longtemps, et avec le plus d'autorité de la réputation
de "toit de la France". Grosso modo, cette croyance a été prise pour vérité
jusqu'à l'avènement des mesures scientifiques de l'ensemble de la chaîne,
c'est à dire vers le premiers tiers du XVIIIe siècle.
Cassini et Maraldi, lors de leur expédition de 1700-1701 ne manquent donc pas
de mesurer à la fois le pic de Canigou et le pic de Saint-Barthélemy (ainsi
que le Madres), afin, même si cela n'est pas explicitement présenté comme cela,
d'établir quel est le plus haut de ces monts et de les départager sans équivoque.
Les mesures sont sans appel, et pour une trentaine d'année, c'est le Canigou qui
se parera du titre de plus haut sommet du royaume. C'est ainsi qu'il faut comprendre
le "Catalogue" qu'ils dressent, des principales montagnes de France (présenté ci-dessus)
et dont la motivation évidente est la recherche de points culminant.
On note toutefois qu'à l'inverse du Mont d'Or, ils se gardent de qualifier
explicitement le Canigou de "plus haute montagne des Pyrénées". Tandis que
la croyance populaire hésitait à attribuer le titre de toit de la France
entre Canigou et Saint-Barthélemy, nos deux se bornent à départager ces
deux monts, mais se gardent bien d'affirmer que tout le reste de la chaîne
est dominé par le Canigou. Mais l'erreur le Cassini et Maraldi consiste à
qualifier le Canigou, Madres et Saint-Barthélemy de "principales montagnes"
en tête de leur catalogue.
|
C'est l'ambiguité contenue dans ce titre qui fera sans doute dire à Buffon
dans son "Histoire Naturelle Générale et Particulière" (1749) qu'il s'agit
là des "plus hautes montagnes de France". L'image ci-contre est un extrait
du tome V de l'Histoire Naturelle de Buffon (p. 304), dans lequel on retrouve
le catalogue de Cassini et Maraldi, mais dont l'intitulé
devient:
"les plus hautes montagnes de France sont les suivantes". Faisant suite
aux données tirées du catalogue publié par Maraldi et Cassini pour
l'Auvergne et le Pyrénées, on trouve une liste de quelques sommets
de Savoie (dont "le mont Blanc ou la Montagne maudite 2213 toises),
et une estimation de la hauteur des
sommets de Suisse (qui "ont de 2400 à 2750 toises de hauteur").
Nul doute que ces écrits prestigieux ont eu valeur d'autorité au moins pendant
un temps, et ont participé à la légende du Canigou "toit de la France".
Cette énumération présentée comme celle des plus hauts sommets de France est d'autant
plus surprenante que dès 1730, de la Blottière avait déjà établi, comme indiqué
ci-dessus, que "les montagnes au-dessus de Mont-Louis [...]sont plus hautes que
le Canigou.
|

|
Extrait de l'"Histoire Naturelle" de Buffon (Tome V, p. 304).
Catalogue des plus hautes montagnes de France.
(cliquer sur l'image pour l'agrandir)
|
|
"Vestiges" des campagnes géodésiques au sommet du pic de Saint-Barthélemy
|
Il subsiste au sommet du Pic de Saint-Barthélemy quelques traces des
diverses campagnes de mesures altimétriques et géodésiques:
- Une inscription "CADASTRE 1828" gravée sur la paroi verticale
sud-est du rocher sommital (voir ci-contre, en haut). Cette inscription
se rapporte probablement aux travaux de cadastre décidés par la Révolution,
mais mis en oeuvre après la fin du premier empire, vers la fin des années 1820.
Néanmoins, d'après Massie (1934), ces levés cadastraux, surtout destinés à
déterminer les superficie en vue de l'assiette foncière, ne se préoccupèrent
pas du tout d'altimétrie:
"Un géomètre triangulateur couvrait le sol d'un réseau de triangles de
700 à 800 mètres de côté. Ensuite, un géomètre arpenteur, sans autre
instrument que la chaine et l'équerre, levait les détails.
Le géomètre-chef vérifiait le travail en recoupant les triangles
par de nouvelles transversales".
- Une ébauche de gravure similaire mais plus petite et inachevée "CADA",
vers l'extrémité orientale de la grande pierre tabulaire du sommet.
Cette inscription inachevée remonte probablement à la même époque.
- A quelques mètres vers l'ouest, une petite figure triangulaire d'une dizaine
de centimètres de côté, gravée près de la base du mât métallique dressé au sommet.
Il pourrait s'agir (à confirmer) d'un repère laissé par la mission menée par Coraboeuf.
-Une embase cimentée (voir ci-contre, en bas), de forme circulaire d'une cinquantaine de centimètres
de diamètre, avec en son centre une partie creuse en forme de cupule,
ayant probablement servi à caler l'extrémité inférieure d'un mât
servant de signal, et portant l'inscription "S.G.A. 1939", enroulée autout du
creux central. Cette inscription se dégrade assez rapidement
d'année en année en s'effritant sous l'effet du gel.
La lettre N est illisible depuis peu.
|
|
| |
Vestige d'une campagne géodésique avec inscription "CADASTRE 1828" gravée dans le rocher, au sommet du pic de Saint-Barthélemy
(cliquer sur l'image pour faire disparaître et réapparaître la surcharge fuschia)
|
|
Vestige d'une campagne géodésique avec inscription "SGN 1939" gravée dans le ciment, au sommet du pic de Saint-Barthélemy
(cliquer sur l'image pour l'agrandir)
|
|
Ces "vestiges" sont remarquables et assez rares, car en général,
les géodésiens sont des gens très discrets, dont le passage au sommet des
montagnes laisse peu de trace (néanmoins, on relève parfois sur les sommets,
une pierre sculptée en forme de borne cubique, d'une vingtaine de cm de côté,
avec une croix en forme de X sur sa face supérieure, servant à indiquer avec
précision la position du signal).
Le sommet officiel actuel du pic de Saint-Barthélemy
Pour connaître où est le point officiel qui représente le sommet du pic, il
faut consulter les documents officiels. Le sommet du pic de Saint-Barthélemy
est un "site" géodésique NTF de premier ordre, baptisé "AXIAT I".
Ce site géodésique comprend quatre points géodésiques,
situés çà et là sur le point sommital du pic (les points géodésiques sont
généralement des clous scellés, ou des croix gravées dans le roc ou sur des bornes).
Chacun peut consulter la
fiche signalétique officielle du site géodésique AXIAT I. Sur cette
fiche on peut alors voir la localisation précise des quatre
points géodésiques (nommés : 1, a, b,c) qui s'y trouvent.
L'altitude officielle du pic est actuellement de 2347.9 m avec une
précision décimétrique.
problème: Cette mesure se réfère au point baptisé (1) dans la liste.
C'est le centre de la croix gravée sur la face supérieure d'un rocher taillé
en forme de borne et scellé sur le haut du rocher sommital (cf. croquis de
la fiche signalétique du site NTF).
Or, ce point, qui représente donc le sommet "officiel" du pic,
a été constaté comme "détruit" par l'IGN en 2003.
En tous cas, cela montre que c'est bien le haut du rocher sommital qui donne
l'altitude officielle du pic, borne ou pas borne.
Noter que le seul point géodésique qui reste côté (donc le seul existant aujourd'hui),
est le point B baptisé "clou scellé dans un bloc de béton marqué SGA 1939",
qui lui, porte l'altitude 2346.4 m.
Ce point se situe donc à 1.40 m en contrebas du vrai sommet.
Bref, de nos jours, le vrai sommet n'est plus représenté par un point côté, et
le seul point côté est en contrebas du sommet d'un bon mètre.
Sources et références
Sources: Maraldi (1703), Cassini(1718), Plantade (1732), Delambre (1810),
Dralet (1813), Reboul (1817), Corabeuf (1832), de Chausenque (1834, 2006),
Cartes d'Etat-Major (1850-1930), Guedj (1997, 2000).
Références: Pour les références complètes de ces ouvrages, voir la page
Références bibliographiques et cartographiques
Page mise à jour le 01/04/2007.